问题
选择题
在△ABC中,A,B,C为内角,且sin Acos A=sin Bcos B,则△ABC是( ).
A.等腰三角形
B.直角三角形
C.等腰直角三角形
D.等腰或直角三角形
答案
答案:D
由sin Acos A=sin Bcos B得sin 2A=sin 2B=sin(π-2B),所以2A=2B或2A=π-2B,即A=B或A+B=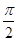 ,所以△ABC为等腰或直角三角形.
,所以△ABC为等腰或直角三角形.
在△ABC中,A,B,C为内角,且sin Acos A=sin Bcos B,则△ABC是( ).
A.等腰三角形
B.直角三角形
C.等腰直角三角形
D.等腰或直角三角形
答案:D
由sin Acos A=sin Bcos B得sin 2A=sin 2B=sin(π-2B),所以2A=2B或2A=π-2B,即A=B或A+B=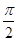 ,所以△ABC为等腰或直角三角形.
,所以△ABC为等腰或直角三角形.