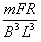问题
计算题
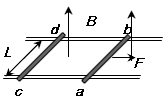
两根足够长的固定的平行金属导轨位于同一水平面内,两导轨间的距离为L,在导轨上面垂直于导轨放置两根导体棒ab和cd,构成矩形回路,如图所示。两根导体棒的质量均为m,电阻均为R,回路中其余部分的电阻可不计。在整个导轨平面内都有竖直向上的匀强磁场,磁感应强度为B,两导体棒均可沿导轨无摩擦地滑行。开始时,固定棒cd,用水平恒力F拉ab棒,使之由静止开始向右加速运动位移为S时,速度恰好达到最大。求:
(1)ab棒所能达到的最大速度是多少?
(2)当ab棒的速度为最大速度的一半时,ab棒的加速度是多少?
(3)当ab棒的速度达到最大速度时,突然撤去力F并同时释放cd棒,从ab开始运动至两棒速度稳定时,电路中 * * 生的热量以及通过导体横截面的电量各是多少?
答案
解:(1)当ab速度最大时,F=F安
F安=BIL
I=BLVm/2R
解得:Vm=2FR/B2L2
(2)当速度为Vm/2,F-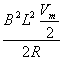 =ma
=ma
解得:a=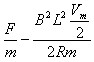 =
=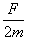
(3)释放cd棒后至两棒共速过程中,动量守恒,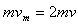
由能量守恒得: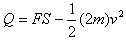
解得: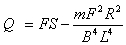
ab由静止开始至速度最大过程中,由法拉第电磁感应定律得:通过导体横截面的电量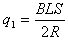
从释放cd棒至两棒共速过程中通过导体横截面的电量q2
对cd棒由动量定理得:BLq2=mv

整个过程中通过导体横截面的总电量q=q1+q2=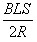 +
+