问题
解答题
求值:sin(-1 200°)·cos 1 290°+cos(-1 020°)·sin(-1 050°)+tan 945°.
答案
2
解:原式=-sin 1 200°·cos 1 290°+cos 1 020°·(-sin 1 050°)+tan 945°=-sin 120°·cos 210°+cos 300°·(-sin 330°)+tan 225°=(-sin 60°)·(-cos 30°)+cos 60°·sin 30°+tan 45°=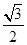 ×
×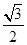 +
+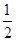 ×
×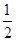 +1=2.
+1=2.
