问题
计算题
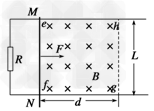
如图所示，光滑的平行金属导轨水平放置，电阻不计，导轨间距为L＝1 m，左侧接一阻值为R＝0.3 Ω的电阻，区域efgh内存在垂直轨道平面向下的有界匀强磁场，磁感应强度为B＝0.5 T，磁场的宽度为d＝1 m；一质量为m＝1 kg、电阻为r＝0.2 Ω的金属棒MN置于导轨上，与导轨垂直且接触良好，受到F＝0.5v＋0.4(N)(v为金属棒的运动速度)的水平力作用，从磁场的左边界ef由静止开始运动，测得电阻两端电压随时间均匀增大．
(1)若撤去水平力后棒的速度v随位移s的变化规律满足v＝v－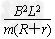
s，且棒在运动到gh处恰好静止，则水平力F作用的时间t为多少？
(2)若在棒未出磁场区域时撤去水平力F，画出棒在整个运动过程中速度v随位移s变化的各种可能的图线．
答案
解：(1)金属棒运动产生电动势：E＝BLv棒和电阻R构成的回路中的电流：I＝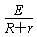
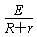
电阻R两端的电压：U＝IR
解得电压U＝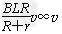
题设U随时间均匀增大，所以v也随时间均匀增大，棒先做匀加速运动：
s1＝
at2
v1＝at
棒受力F＝0.5v＋0.4和安培阻力FA＝BIL，由牛顿第二定律得：(0.5v＋0.4)－BIL＝ma
又I＝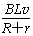
所以0.5v1＋0.4－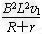
＝ma
撤去外力后棒做减速运动，由题设v＝v0－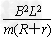
s得：0＝v1－
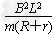s2
全程运动：s1＋s2＝d
将已知条件代入以上方程解得：0.2t2＋0.8t－1＝0
解得力F作用的时间t＝1 s
(2)可能图线如下：
