阅读下面对话,判断正(T)误(F)。
A: Hello!
B: Hello! What's your name?
A: My name is Wang Lin. What about you?
B: My name is Wei Hua. How are you?
A: I'm fine, thank you. And you?
B: I'm fine, too. What grade are you in, Wang Lin?
A: I'm in Grade One. Are you in Grade One,too?
B: No, I'm in Grade Two. How old are you?
A: I'm eleven. What about you?
B: I'm one year older than you.
A: Oh! What is in your hand?
B: It is an orange.
A: Can you spell it?
B: Yes, O-R-A-N-G-E, orange.
( )1. Wang Lin is in Grade Two.
( )2. Wei Hua is in Grade one.
( )3. Wang Lin is eleven.
( )4. Wei Hua is twelve.
( )5. There is an orange in Wang Lin's hand.

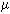 F,有一匀强磁场,方向垂直导轨PQ、MN所在平面向下,如图所示,磁感强度为B=0.5T.(除导轨PQ、MN和金属杆ab外其余部分都是绝缘的)当闭合电键K时,ab杆将从导轨上冲出,并沿光滑斜面升到高为0.2m处,这过程电容器两端电压减小了一半,求:
F,有一匀强磁场,方向垂直导轨PQ、MN所在平面向下,如图所示,磁感强度为B=0.5T.(除导轨PQ、MN和金属杆ab外其余部分都是绝缘的)当闭合电键K时,ab杆将从导轨上冲出,并沿光滑斜面升到高为0.2m处,这过程电容器两端电压减小了一半,求: