问题
计算题
如图所示,两根足够长、电阻不计的平行光滑金属导轨相距为L,导轨平面与水平面成θ角,质量均为m、阻值均为R的金属棒a、b紧挨着放在两导轨上,整个装置处于垂直于导轨平面的匀强磁场中,磁感应强度大小为B,一平行于导轨平面向上F=2mgsinθ的恒力拉a棒,b棒同时静止释放,直至b棒刚好匀速时,在此过程中通过棒的电量为q,(棒与导轨始终垂直并保持良好接触,重力加速度为g),求:
(1)b棒刚好匀速时,a、b棒间的距离s;
(2)b棒最终的速度大小vb;
(3)此过程中a棒产生的热量Q。

答案
解:(1)根据电磁感应定律有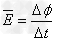 ①
①
根据闭合电路欧姆定律有 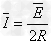 ②
②
又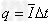 ③
③
得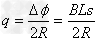
解得: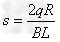 ④
④
(2)b棒匀速时BIL = mgsin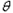 ⑤
⑤
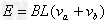 ⑥
⑥
I =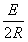 ⑦
⑦
对a棒由牛顿第二定律得: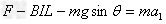
即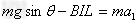 ⑧
⑧
对b棒由牛顿第二定律得: ⑨
⑨
由⑧⑨式可得a1=a2
故a、b棒运动规律相似,速度同时达到最大,且最终va=vb ⑩
由⑤⑥⑦⑩式可得vb= 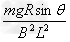
(3)因a、b棒串联,产生的热量相同,设a、b棒在此过程中运动的距离分别为s1和s2,对a、b棒组成的系统,由功能关系得:

s1+ s2=s
解得: