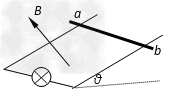
如图所示,光滑足够长导轨倾斜放置,导轨间距为L=1m,导轨平面与水平面夹角为θ=30°,其下端连接一个灯泡,灯泡电阻为R=2Ω,导体棒ab垂直于导轨放置,除灯泡外其它电阻不计。两导轨间的匀强磁场的磁感应强度为B=0.5T,方向垂直于导轨所在平面向上。将导体棒从静止释放,在导体棒的速度v达到2m/s的过程中通过灯泡的电量q=2C。随着导体棒的下滑,其位移x随时间t的变化关系趋近于x=4t-2(m)。取g=10m/s2,求:
(1)导体棒的质量m;
(2)当导体棒速度为v=2m/s时,灯泡产生的热量Q;
(3)辨析题:为了提高ab棒下滑过程中小灯泡的最大功率,试通过计算提出两条可行的措施。
某同学解答如下:小灯泡的最大功率为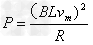 (其中vm为下滑的最大速度),因此提高ab棒下滑过程中小灯泡的最大功率的措施有:增大磁感应强度B、……。由此所得结果是否正确?若正确,请写出其他两条可行的措施;若不正确,请说明理由并给出正确的解答。
(其中vm为下滑的最大速度),因此提高ab棒下滑过程中小灯泡的最大功率的措施有:增大磁感应强度B、……。由此所得结果是否正确?若正确,请写出其他两条可行的措施;若不正确,请说明理由并给出正确的解答。
解:(1)根据x=4t-2(m)得,最后匀速运动的速度为vm=4m/s
匀速运动时,F安=mgsin30°
B2L2vm/R=mgsin30°
解得m=0.1kg
(2)通过灯泡的电量q=It=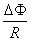 =
=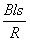 =2c
=2c
解得s=8m
由动能定理得mgssin30°-W安=mv2/2
灯泡产生的热量Q=W安= mgssin30°-mv2/2=3.8J
(3)不正确,式中vm,根据安培力等于重力的下滑力,可以求出它与B的平方成反比,所以增大B的同时,最大速度在减小,并不能提高小灯泡的最大功率
因为P=I2R,所以提高ab棒下滑过程中小灯泡的最大功率,须增大电流I或电阻R匀速运动时,F安=BIL=mgsinθ
I=mgsinθ/BL
所以可以减小B、L,或增大m、R、θ
