问题
解答题
三角形中位线定理,是我们非常熟悉的定理.
①请你在下面的横线上,完整地叙述出这个定理:______.
②根据这个定理画出图形,写出已知和求证,并对该定理给出证明.
答案
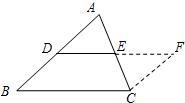
(1)三角形的中位线平行于第三边且等于第三边的一半.
(2)已知:DE是△ABC的中位线,
求证:DE∥BC,DE=
BC.1 2
证明:延长DE到F,使EF=DE,连接CF.
∵AE=CE,∠AED=∠CEF,
∴△ADE≌△CEF.
∴AD=CF,∠ADE=∠CFE.
∴AD∥CF.
∵AD=BD,
∴BD=CF.
∴四边形BCFD是平行四边形.
∴DE∥BC,DE=
BC.1 2
故答案为三角形的中位线平行于第三边且等于第三边的一半.
