问题
计算题
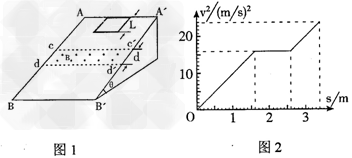
个质量m＝0.1kg的正方形金属框总电阻R＝0.5Ω，金属框放在表面是绝缘且光滑的斜面顶端，自静止开始沿斜面下滑，下滑过程中穿过一段边界与斜面底边BB'平行、宽度为d的匀强磁场后滑至斜面底端BB'，设金属框在下滑时即时速度为v，与此对应的位移为s，那么v2-s图像如图2所示，已知匀强磁场方向垂直斜面向上。试问：
（1）分析v2-s图像所提供的信息，计算出斜面倾角θ和匀强磁场宽度d。
（2）匀强磁场的磁感应强度多大？
（3）金属框从斜面顶端滑至底端所需的时间为多少？
（4）现用平行斜面沿斜面向上的恒力F作用在金属框上，使金属框从斜面底端BB'静止开始沿斜面向上运动，匀速通过磁场区域后到达斜面顶端。试计算恒力F做功的最小值。
答案
解：（1）s＝0到s＝1.6 m由公式v2＝2as
该段图线斜率k＝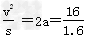
＝10，所以a＝5m
根据牛顿第二定律mgsinθ＝ma，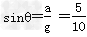
＝0.5，θ＝30°
由图得从线框下边进磁场到上边出磁场均做匀速运动，所以△s＝2L＝2d＝（2.6－1.6）m＝1 m，d＝L＝0.5m
（2）线框通过磁场时，v12＝16，v1＝4 m/s
此时F安＝mgsinθ，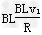
＝mgsinθ，
＝0.5 T
（3）
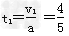s＝0.8 s
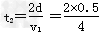s＝0.25 s
s3＝（3.4－2.6）m＝0.8 m
s3＝v1t3＋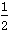
at32，t3＝0.2 s
所以t＝t1＋t2＋t3＝（0.8＋0.25＋0.2）s＝1.25 s
（4）未入磁场F－mgsinθ＝ma2，进入磁场F＝mgsinθ＋F安
∴F安＝ma2，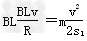
，v＝
＝2 m/s，F安＝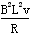
＝0.25N
最小功WF＝2dF安＋mg（s1＋s2＋s3）sinθ＝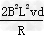
＋mg（s1＋s2＋s3）sinθ＝1.95 J