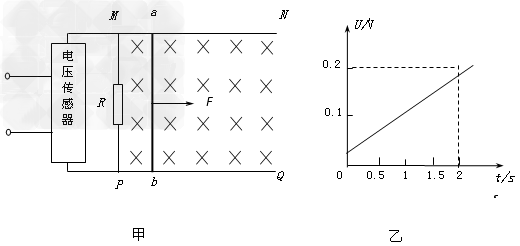
如图甲所示,光滑且足够长的平行金属导轨MN、PQ固定在同一水平面上,两导轨间距L=0.30m。导轨电阻忽略不计,其间连接有固定电阻R=0.40Ω。导轨上停放一质量m=0.10kg、电阻r=0.20Ω的金属杆ab,整个装置处于磁感应强度B=0.50T的匀强磁场中,磁场方向竖直向下。用一外力F沿水平方向拉金属杆ab,使之由静止开始运动,利用电压传感器测得R两端的电压U随时间t变化的关系如图乙所示。
(1)证明金属杆做匀加速直线运动,并计算加速度的大小;
(2)求第1s末外力F的瞬时功率;
(3)如果水平外力从静止开始拉动杆2s所做的功W=0.35J,求金属杆上产生的焦耳热。
解:(1)设路端电压为U,金属杆的运动速度为v,则
感应电动势E= BLv
通过电阻R 的电流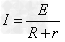
电阻R两端的电压U=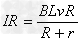
由图乙可得U=kt,k=0.10V/s
解得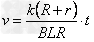
因为速度与时间成正比,所以金属杆做匀加速运动,加速度
(2)在2s末,速度v2=at=2.0m/s,电动势E=BLv2
通过金属杆的电流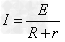
金属杆受安培力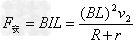
解得:F=7.5×10-2 N
设2s末外力大小为F2,由牛顿第二定律,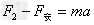
解得:F2=1.75×10-2 N
故2s末时F的瞬时功率P=F2v2=0.35W
(3)设回路产生的焦耳热为Q,由能量守恒定律,W=Q+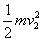
解得:Q=0.15J
电阻R与金属杆的电阻r串联,产生焦耳热与电阻成正比
所以,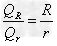
运用合比定理, ,而
,而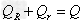
故在金属杆上产生的焦耳热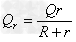
解得:Qr=5.0×10-2 J
