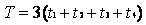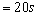问题
计算题
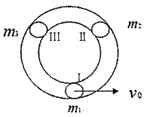
一水平放置的圆环形钢性窄槽固定在桌面上,槽内嵌着三个大小相同的钢性小球,它们的质量分别为m1、m2、m3,且m2=m3=2m1。小球与槽的两壁刚好接触且不计所有摩擦。起初三个小球处于如图所示的等间距的Ⅰ、Ⅱ、Ⅲ三个位置,m2、m3静止,m1以初速度v0= 沿槽运动,R为圆环内半径与小球半径之和。已知m1以v0与静止的m2碰撞之后,m2的速度大小为2v0/3;m2与m3碰撞之后二者交换速度;m3与m1之间的碰撞为弹性碰撞。求此系统的运动周期T。
沿槽运动,R为圆环内半径与小球半径之和。已知m1以v0与静止的m2碰撞之后,m2的速度大小为2v0/3;m2与m3碰撞之后二者交换速度;m3与m1之间的碰撞为弹性碰撞。求此系统的运动周期T。
答案
解:设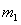 经过
经过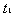 与
与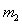 相碰,
相碰,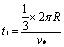
设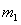 与
与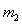 碰撞之后两球的速度分别为
碰撞之后两球的速度分别为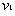 、
、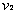 ,在碰撞过程中由动量守恒定律得:
,在碰撞过程中由动量守恒定律得:
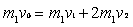
因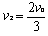 ,求得
,求得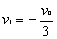 ,方向与碰前速度方向相反
,方向与碰前速度方向相反
设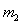 经过
经过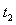 与
与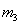 相碰,
相碰,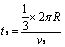
设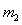 与
与 碰撞之后两球的速度分别为
碰撞之后两球的速度分别为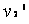 、
、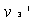 ,因
,因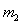 与
与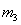 在碰撞后交换速度
在碰撞后交换速度
所以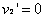 ,
,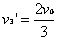
由碰后速度关系知,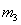 与
与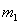 碰撞的位置在Ⅰ位置,设
碰撞的位置在Ⅰ位置,设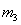 经过
经过 与
与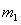 相碰,
相碰,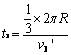
设 与
与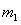 碰撞后的速度分别为
碰撞后的速度分别为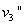 ,
,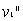 ,由动量守恒和机械能守恒定律可得:
,由动量守恒和机械能守恒定律可得:
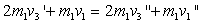
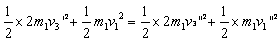
联立得: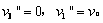 或
或 (舍)
(舍)
设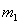 碰后经
碰后经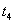 回到Ⅱ位置,
回到Ⅱ位置,
至此,三个小球相对于原位置分别改变了120°,且速度与最初状态相同。故再经过两个相同的过程,即完成一个系统的运动周期