问题
计算题
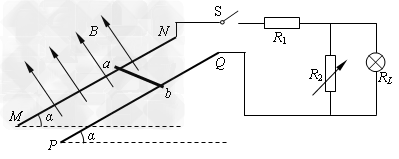
如图所示，两足够长平行光滑的金属导轨MN、PQ相距为L，导轨平面与水平面夹角为α，导轨电阻不计。磁感应强度为B的匀强磁场垂直导轨平面斜向上，长为L的金属棒ab垂直于MN、PQ放置在导轨上，且始终与导轨接触良好，金属棒的质量为m、电阻为R。两金属导轨的上端连接右侧电路，电路中R2为一电阻箱，已知灯泡的电阻RL＝4R，定值电阻R1＝2R，调节电阻箱使R2＝12R，重力加速度为g，闭合开关S，现将金属棒由静止释放，求：
（1）金属棒下滑的最大速度vm；
（2）当金属棒下滑距离为s0时速度恰好达到最大，则金属棒由静止开始下滑2s0的过程中，整个电路产生的电热；
（3）改变电阻箱R2的值，当R2为何值时，金属棒达到匀速下滑时R2消耗的功率最大。
答案
解：（1）当金属棒匀速下滑时速度最大，达到最大时有
mgsina＝F安 ①
F安＝BIL ②
I＝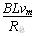
③
其中R总＝6R ④
联立①～④式得金属棒下滑的最大速度vm＝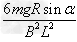
⑤
（2）由动能定理WG－W安＝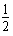
mvm2 ⑥
由于WG=2mgs0sinα，W安= Q
解得Q＝2mgs0sinα－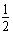
mvm2
将⑤代入上式可得Q＝2mgs0sinα－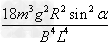
也可用能量转化和守恒求解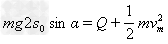
再将⑤式代入上式得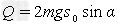
-
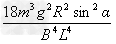
（3）∵金属棒匀速下滑
∴mgsinα= BIL ⑦
P2=I22R2 ⑧
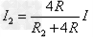
联立得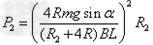
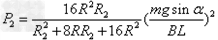
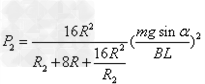
当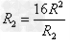
，即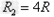
时，R2消耗的功率最大