问题
计算题
如图所示，在光滑水平面上有一质量为M的长木板，长木板上有一质量为m的小物块，它与长木板间的动摩擦因数为μ。开始时，长木板与小物块均靠在与水平面垂直的固定挡板处，某时刻它们以共同的速度v0向右运动，当长木板与右边的固定竖直挡板碰撞后，其速度的大小不变、方向相反，以后每次的碰撞均如此。设左右挡板之间的距离足够长，且M＞m。
（1）要想物块不从长木板上落下，则长木板的长度L应满足什么条件？
（2）若上述条件满足，且M＝2 kg，m＝1 kg，v0＝10 m/s，求整个系统在第5次碰撞前损失的所有机械能。
答案
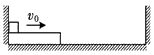
解：（1）设第1次碰撞后小物块与长木板共同运动的速度为v1，第n次碰撞后小物块与长木板共同运动的速度为vn。每次碰撞后，由于两挡板的距离足够长，物块与长木板都能达到相对静止，第1次若不能掉下，往后每次相对滑动的距离会越来越小，更不可能掉下。由动量守恒定律和能量守恒定律有：
(M－m)v0＝(M＋m)v1
μmgs＝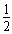
(m＋M)v02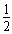－(M＋m)v12
解得：s＝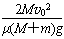
故L应满足的条件是：L≥s＝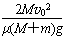
（2）第2次碰撞前有：(M－m)v0＝(M＋m)v1
第3次碰撞前有：(M－m)v1＝(M＋m)v2
第n次碰撞前有：(M－m)vn－2＝(M＋m)vn－1
所以vn－1＝(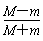
)n－1v0
故第5次碰撞前有：v4＝(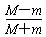
)4v0
故第5次碰撞前损失的总机械能为：ΔE＝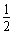
(M＋m)v02－
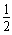(M＋m)v42
代入数据解得：ΔE＝149.98 J