问题
问答题
一对无限长平行导轨位于竖直平面内，轨道上串联一电容器C（开始未充电）.另一根质量为m的金属棒ab可沿导轨下滑，导轨宽度为L，在讨论的空间范围内有磁感应强度为B、方向垂直整个导轨平面的匀强磁场，整个系统的电阻可以忽略，ab棒由静止开始下滑，求它下滑h高度时的速度v.
答案
v=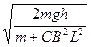
解决该题的关键是分析清楚ab棒的运动规律，若设ab棒下滑过程中某一瞬时加速度为ai，则经过一微小的时间间隔Δt，其速度的增加量为Δv=ai·Δt.
棒中产生的感应电动势的增加量为：ΔE=BLΔv=BLai·Δt
电容器的极板间电势差的增加量为：ΔUi=ΔE=BLai·Δt
电容器电荷量的增加量为：ΔQ=C·ΔU=CBLai·Δt
电路中的充电电流为：I=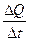
=CBLai
ab棒所受的安培力为：F=BLI=CB2L2ai
由牛顿第二定律得：mg-F=mai，即mg-CB2L2ai=mai，所以，ai=
，可见，棒的加速度与时间无关，是一个常量，即棒ab向下做匀加速直线运动.所以要求的速度为v=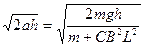
.