如图所示,两平行的足够长的金属导轨间距为L,导轨与水平面成30°角。质量为m,长为L,电阻为r的两个完全相同的金属棒ab、cd放置在导轨上,恰好均处于静止状态。整个装置处于匀强磁场中,磁感应强度为B,磁场方向与导轨平面垂直向上。现用沿导轨向上的外力施与金属棒ab上,使ab棒由静止开始沿导轨向上做匀加速运动,加速度为a。则(滑动摩擦力与最大静摩擦力近似相等)

⑴ 金属棒与导轨间的动摩擦因数是多少?
⑵ 要使金属棒cd始终静止在导轨上,金属棒ab运动的速度不能超过多少?
⑶ 在金属棒ab由静止到达(2)中速度的过程中外力和安培力做的总功是多少?
(1) 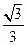 (2)
(2)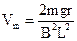 ⑶
⑶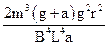
⑴对金属棒cd进行受力分析如图所示
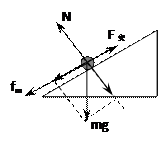
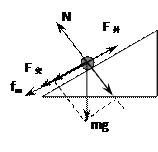
棒cd恰好静止,此时摩擦力为最大静摩擦力,根据平衡条件可得
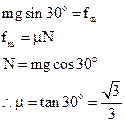
即动摩擦因数为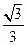 ┅┅┅┅(3分)
┅┅┅┅(3分)
⑵当ab棒开始运动后切割磁感线产生电动势cd棒受到安培力的作用,随着ab棒运动的速度增大,安培力也增大,cd棒受到的摩擦力逐渐减小,随着安培力的继续增大,摩擦力变为反方向,当摩擦力逐渐增大达到最大摩擦力时,ab棒运动的速度达到最大,根据平衡条件有
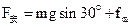 ┅┅┅┅(1分)
┅┅┅┅(1分)

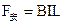 ┅┅┅┅(1分)
┅┅┅┅(1分)
ab棒切割磁感线产生的电动势
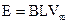 ┅┅┅┅(1分)
┅┅┅┅(1分)
回路中的电流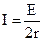 ┅┅┅┅(1分)
┅┅┅┅(1分)
联立以上各式可得ab棒的最大速度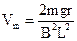 ┅┅┅┅(1分)
┅┅┅┅(1分)
⑶对ab棒受力分析如右图所示,棒做匀加速运动
运动的位移  ┅┅┅┅(1分)
┅┅┅┅(1分)
根据动能定理可得
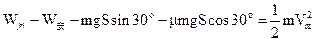
┅┅┅┅(2分)
则外力和安培力做的总功为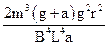
┅┅┅┅(2分)
