问题
计算题
光滑水平面上,用弹簧相连接的质量均为2 kg的A、B两物体都以v0=6 m/s速度向右运动,弹簧处于原长。质量为4 kg的物体C静止在前方,如图所示,B与C发生碰撞后粘合在一起运动,在以后的运动中,求:
(1)弹性势能最大值为多少?
(2)当A的速度为零时,弹簧的弹性势能为多少?
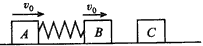
答案
解:(1)B、C碰撞瞬间,B、C的总动量守恒,由动量守恒定律得:
mBv0=(mB+mC)v
v=2 m/s
三个物体速度相同时弹性势能最大,由动量守恒定律得:
mAv0+mBv0= (mA+mB+mC)v共
v共=3m/s
设最大弹性势能为Ep,由能量守恒得:
 12 J
12 J
(2)当A的速度为零时,由动量定恒定律得:
mAv0+mBv0=(mB+mC)vBC
vBC=4 m/s
则此时的弹性势能
