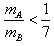问题
计算题
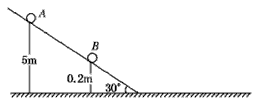
倾角为30°的足够长光滑斜面下端与一足够长光滑水平面相接，连接处用一光滑小圆弧过渡，斜面上距水平面高度分别为h1=5 m和h2=0.2 m的两点上，各固定一小球A和B。某时刻由静止开始释放A球，经过一段时间t后，同样由静止开始释放B球。g取10 m/s2，则：
(1)为了保证A、B两球不会在斜面上相碰，t最长不能超过多少？
(2)在满足(1)的情况下，为了保证两球在水平面上的碰撞次数不少于两次，两球的质量mA和mB应满足什么条件？(假设两球的碰撞过程没有能量损失)
答案
解：(1)设两球在斜面上下滑的加速度为a，根据牛顿第二定律得：mgsin30°=ma
设A、B两球下滑到斜面底端所用时间分别为t1和t2，则：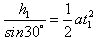
，
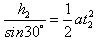
所以：t=t1-t2=1.6 s
(2)设A、B两球下滑到斜面底端时速度分别为v1和v2，第一次相碰后速度分别为vA和vB，则根据机械能守恒：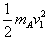
=mAgh1 ①，
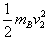=mBgh2 ②
根据动量守恒和能量守恒
mAv1+mBv2=mAvA+mBvB ③
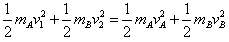④
为使两球能发生第二次碰撞，应满足vA<0且|vA|>vB ⑤
由①②③④⑤代入数据后可得：