如图所示,倾角为θ的足够长的光滑绝缘斜面上存在宽度均为L的匀强磁场和匀强电场区域,磁场的下边界与电场的上边界相距为3L,其中电场方向沿斜面向上,磁场方向垂直于斜面向下、磁感应强度的大小为B。电荷量为q的带正电小球(视为质点)通过长度为L的绝缘轻杆与边长为L、电阻为R的正方形单匝线框相连,组成总质量为m的“ ”型装置,置于斜面上,线框下边与磁场的上边界重合。现将该装置由静止释放,当线框下边刚离开磁场时恰好做匀速运动;当小球运动到电场的下边界时刚好返回。已知L=1m,B=0.8T,q=2.2×10-6C,R=0.1Ω,m=0.8kg,θ=53°,sin53°=0.8,g取10m/s2。求:

⑴线框做匀速运动时的速度大小;
⑵电场强度的大小;
⑶正方形单匝线框中产生的总焦耳热.
(1) 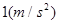 (2)
(2) (3)
(3)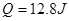
题目分析:(1)解:设线框做匀速运动时的速度大小V

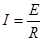
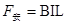 则
则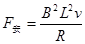 3分
3分
由平衡条件 ·2分
·2分
解得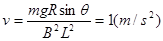 1分
1分
(2)从线框刚离开磁场区域到小球运动到电场下边界的过程
由动能定理 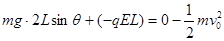 4分
4分
解得: 2分
2分
(3)经足够长的时间后,线框上边运动到磁场区域的下边界时速度恰为零,此后线框不再进入磁场,不再产生焦耳热。从开始运动到该状态,由能量守恒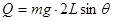 2分
2分
解得: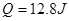
点评:当线框产生感应电流时,由安培力做功从而产生热量.因安培力不恒定,所以运用动能定理求得产生的热量.
