问题
计算题
如图所示，两根相距L平行放置的光滑导电轨道，与水平面的夹角均为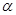 
，轨道间有电阻R，处于磁感应强度为B、方向竖直向上的匀强磁场中，一根质量为m、电阻为r的金属杆ab，由静止开始沿导电轨道下滑．设下滑中ab杆始终与轨道保持垂直，且接触良好，导电轨道有足够的长度，且电阻不计．求：
(1)ab杆将做什么运动 ？若开始时就给ab沿轨道向下的拉力F使其由静止开始向下做加速度为a的匀加速运动 (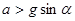
)．求拉力F与时间t的关系式．
答案
金属杆做匀速运动 F＝m(a－gsinα)＋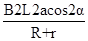
·t
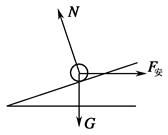
题目分析：(1)金属杆受力如图所示，当金属杆向下滑动时，速度越来越大，安培力F安变大，金属杆加速度变小．随着速度的变大，加速度越来越小．ab做加速度越来越小的加速运动，最终加速度变为零，金属杆做匀速运动．
(2)经过时间t，ab杆速度v＝at，感应电流I＝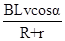
由牛顿第二定律F＋mgsinα－BILcosα＝ma
F＝m(a－gsinα)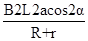＋·t.
点评：解决本题的关键会根据牛顿第二定律结合运动学能够分析出金属棒的运动情况，当a=0时，速度达到最大．
