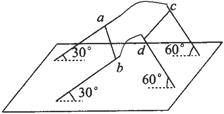
(13分)如图所示,左右两边分别有两根平行金属导轨相距为L,左导轨与水平面夹30°角,右导轨与水平面夹60°角,左右导轨上端用导线连接。导轨空间内存在匀强磁场,左边的导轨处在方向沿左导轨平面向下,磁感应强度大小为B的磁场中。右边的导轨处在垂直于右导轨斜向上,磁感应强度大小也为B的磁场中。质量均为m的导杆ab和cd垂直导轨分别放于左右两侧导轨上,已知两导杆与两侧导轨间动摩擦因数均为μ=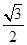 ,回路电阻恒为R,若同时无初速释放两导杆,发现cd沿右导轨下滑
,回路电阻恒为R,若同时无初速释放两导杆,发现cd沿右导轨下滑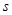 距离时,ab杆才开始运动。(认为最大静摩擦力等于滑动摩擦力)。
距离时,ab杆才开始运动。(认为最大静摩擦力等于滑动摩擦力)。
(1)试求ab杆刚要开始运动时cd棒的速度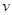
(2)以上过程中,回路中 * * 生多少焦耳热?
(3)cd棒的最终速度为多少?
(1)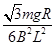 (2)
(2)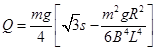 (3)
(3)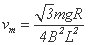
题目分析:(1)ab杆刚运动时,有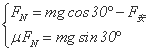 ∴F安=
∴F安=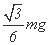 (3分)
(3分)
由安培力公式F安=BIL得I=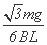 (1分)
(1分)
由闭合电路欧姆定律得E=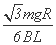 (1分)
(1分)
对cd杆由法拉第电磁感应定律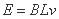 ,∴
,∴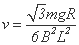 (1分)
(1分)
(2)由动能定理有:mgssin60°-μmgscos60°-W克安=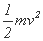 (2分)
(2分)
W克安=Q (1分)
故:Q=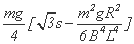 (1分)
(1分)
(3)mgsin60°-μmgcos60°=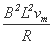 (2分)
(2分)
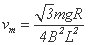 (1分)
(1分)
