阅读下面的文言文,完成题
丘处机传
丘处机,登州栖霞人,自号长春子。儿时,有相者谓其异日当为神仙宗伯。年十九,为全真学于宁海之昆仑山,与马钰、谭处端、刘处玄、王处一、郝大通、孙不二同师重阳王真人。重阳一见处机,大器之。金、宋之季,俱遣使来召,不赴。
岁己卯,太祖自乃蛮命近臣札八儿、刘仲禄持诏求之。处机一日忽语其徒,使促装,曰:“天使来召我,我当往。”翌日,二人者至,处机乃与弟子十有八人同往见焉。明年,宿留山北,先驰表谢,拳拳以止杀为劝。又明年,趣使再至,乃发抚州,经数十国,为地万有余里。盖蹀血战场,避寇叛域,绝粮沙漠,自昆仑历四载而始达雪山。常马行深雪中,马上举策试之,未及积雪之半。既见,太祖大悦,赐食、设庐帐甚饬。
太祖时方西征,日事攻战,处机每言欲一天下者,必在乎不嗜杀人。及问为治之方,则对以敬天爱民为本。问长生久视之道,则告以清心寡欲为要。太祖深契其言,曰:“天锡仙翁,以寤朕志。”命左右书之,且以训诸子焉。于是锡之虎符,副以玺书,不斥其名,惟曰“神仙”。一日雷震,太祖以问,处机对曰:“雷,天威也。人罪莫大于不孝,不孝则不顺乎天,故天威震动以警之。似闻境内不孝者多,陛下宜明天威,以导有众。”太祖从之。岁癸未,太祖大猎于东山,马踣,处机请曰:“天道好生,陛下春秋高,数畋猎,非宜。”太祖为罢猎者久之。时国兵践蹂中原,河南、北尤甚,民罹俘戮,无所逃命。处机还燕,使其徒持牒招求于战伐之余,由是为人奴者得复为良,与滨死而得更生者,毋虑二三万人。中州人至今称道之。
岁乙酉,荧惑犯尾,其占在燕,处机祷之,果退舍。丁亥,又为旱祷,期以三日雨,当名瑞应,已而亦验。有旨改赐宫名曰长春,且遣使劳问,制若曰:“朕常念神仙,神仙毋忘朕也。” 六月,浴于东溪。越二日,天大雷雨,太液池岸北水入东湖,声闻数里,鱼鳖尽去,池遂涸,而北口高岸亦崩。处机叹曰:“山其摧乎,池其涸乎,吾将与之俱乎!”遂卒,年八十。其徒尹志平等世奉玺书袭掌其教,至大间加赐金印。
(选自《元史·卷二百二·列传第八十九》)
小题1:对下列句子中加点的词的解释,不正确的一项是( )
A.重阳一见处机,大器之器:重视
B.太祖大悦,赐食、设庐帐甚饬饬:恭谨
C.太祖大猎于东山,马踣踣:跌倒
D.数畋猎,非宜数:数目小题2:下列各组句子中,加点词用法和意义都相同的一项是 ( )
A.为全真学于宁海之昆仑山莫之能御也
B.故天威震动以警之以若所为,求若所欲
C.人罪莫大于不孝构怨于诸侯
D.与滨死而得更生者举世而非之而不加沮小题3:下列各组语句中,全都表明丘处机爱护百姓的一组是( )
①金、宋之季,俱遣使来召,不赴 ②先驰表谢,拳拳以止杀为劝
③蹀血战场,避寇叛域,绝粮沙漠 ④每言欲一天下者,必在乎不嗜杀人
⑤使其徒持牒招求于战伐之余 ⑥山其摧乎,池其涸乎,吾将与之俱乎
A.①③⑤
B.②④⑤
C.①④⑥
D.②④⑥小题4:下列对原文有关内容的分析和概括,正确的一项是( )
A.丘处机十九岁时出家,皈依在王重阳真人门下,成为王真人嫡传的“全真七子”中的大师兄。
B.在拒绝金、宋朝廷的征召后,丘处机与十八名弟子一行不远万里,历经艰辛,历经四年抵达成吉思汗驻地,他们此行意在止杀,为此甚至在雪地里都经常拿起经卷彼此讨论。
C.当成吉思汗向丘处机询问长生之术时,丘处机坦言关键在于清心寡欲。成吉思汗非但没有责怪丘处机,反而极为敬重他,赐给他虎符和玺书,尊称他为“神仙”。
D.凭着虎符和玺书,丘处机师徒借入教的名义拯救了大量汉人,受到百姓称赞。其后,丘处机的祈祷使不利于燕地的煞星移位,使干旱的地区下了三天雨,造福于百姓。小题5:将下列句子翻译成现代汉语(6分)
(1)王若隐其无罪而就死地,则牛羊何择焉?(3分)
(2)此惟救死而恐不赡,奚暇治礼仪哉?(3分)

 v
v
 sin θ
sin θ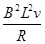 =ma,分析可得ab棒做加速度减小的加速运动,故其平均速度不等于初末速度的平均值,A错误;设ab棒沿斜面下滑的位移为x,则电荷量q=IΔt=
=ma,分析可得ab棒做加速度减小的加速运动,故其平均速度不等于初末速度的平均值,A错误;设ab棒沿斜面下滑的位移为x,则电荷量q=IΔt=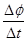 ·
·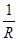 Δt=
Δt=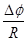 =
=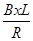 ,解得位移x=
,解得位移x=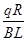 ,B正确;根据能量守恒定律可知,产生的焦耳热等于ab棒机械能的减少量,Q=
,B正确;根据能量守恒定律可知,产生的焦耳热等于ab棒机械能的减少量,Q= -
-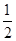 mv2,ab棒受到的最大安培力为
mv2,ab棒受到的最大安培力为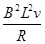 ,C、D错误.
,C、D错误.