问题
计算题
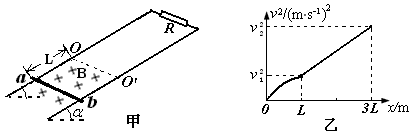
如甲图所示，相距为L的光滑平行金属导轨与水平面的夹角为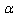
，导轨一部分处在垂直导轨平面的匀强磁场中，OO'为磁场边界，磁感应强度为B，导轨右端接有定值电阻R，导轨电阻忽略不计。在距OO'为L处垂直导轨放置一质量为m、电阻不计的金属杆ab。
（1）若ab杆在平行于斜面的恒力作用下由静止开始沿斜面向上运动，其速度平方一位移关系图像如乙图所示，图中v1和v2为已知。则在发生3L位移的过程中，电阻R上产生的电热Q1是多少？
（2）ab杆在离开磁场前瞬间的加速度是多少？
（3）若磁感应强度B＝B0＋kt（k为大于0的常数），要使金属杆ab始终静止在导轨上的初始位置，试分析求出施加在ab杆的平行于斜面的外力。
答案
解：（1）物体的位移为3L，在0-L段，恒力F、重力mg及安培力F安对物体做功，安培力的功等于电阻上产生的电热Q1，由动能定理：
FL－mgLsina＋W安＝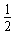
mv12
而W安＝－Q1
在L-3L段，由动能定理得：
（F－mgsina）2L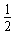＝mv2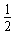2－mv12
解得Q1＝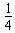
m（v22－3v12）
（2）ab杆在离开磁场前瞬间，沿轨道方向受重力分力mgsina、安培力F安和恒力F作用
解得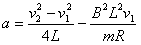
（3）当磁场按B＝B0＋kt规律变化时，由于ab静止在导轨上的初始位置，所以感应电动势为：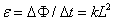
安培力为：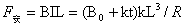
由平衡条件得：
解得：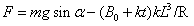
①若
时，F的方向沿斜面向下
②若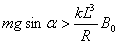
时，F的方向先沿斜面向上，当经过
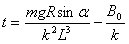时，F的方向又将变为沿斜面向下