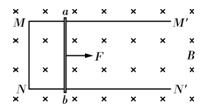
如图所示,M′MNN′为放置在粗糙绝缘水平面上的U型金属框架,MM′和NN′相互平行且足够长,间距l=0.40m,质量M=0.20kg。质量m=0.10kg的导体棒ab垂直于MM′和NN′放在框架上,导体棒与框架的摩擦忽略不计。整个装置处于竖直向下的匀磁场中,磁感应强度B=0.50T。t=0时,垂直于导体棒ab施加一水平向右的恒力F=2.0N,导体棒ab从静止开始运动;当t=t1时,金属框架将要开始运动,此时导体棒的速度v1=6.0m/s;经过一段时间,当t=t2时,导体棒ab的速度v2=12.0m/s;金属框架的速度v3=0.5m/s。在运动过程中,导体棒ab始终与MM′和NN′垂直且接触良好。已知导体棒ab的电阻r=0.30Ω,框架MN部分的阻值R=0.10Ω,其余电阻不计。设框架与水平面间的最大静摩擦力等于滑动摩擦力,g取10m/s2。求:
(1)求动摩擦因数μ;
(2)当t=t2时,求金属框架的加速度;
(3)若在0~t1这段时间内,MN上产生的热量 Q=0.10J,求该过程中导体棒ab位移x的 大小。
(1)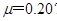 (2)
(2)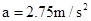 (3)
(3)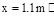
题目分析:(1)当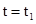 时,导体棒ab切割磁感线产生的感应电动势
时,导体棒ab切割磁感线产生的感应电动势
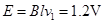
所以回路中的电流
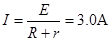
取金属框架为研究对象,MN边受到安培力,
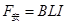 (1分)
(1分)
与地面之间的最大静摩擦力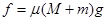
刚要开始滑动说明安培力等于最大静摩擦力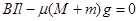 (1分)
(1分)
解得: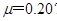 (1分)
(1分)
(2)当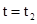 时,设回路中的电流为
时,设回路中的电流为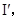
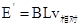 (1分)
(1分)
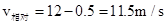
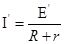

取金属框架为研究对象,根据牛顿第二定律有
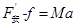
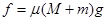
解得: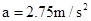 (1分)
(1分)
(3)在0~t1时间内,电路中产生的总热量
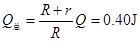 (1分)
(1分)
根据功能原理,拉力做功转化为焦耳热和金属棒动能
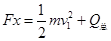 (1分)
(1分)
解得: 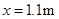 (1分)
(1分)
