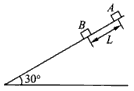
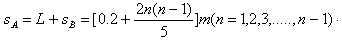如图所示，在倾角θ=30°、足够长的斜面上分别固定着两个相距L=0.2 m的物体A、B，它们的质量mA=mB=1 kg，与斜面间的动摩擦因数分别为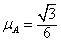
和
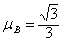。在t=0时刻同时撤去固定两物体的外力后，A物体将沿斜面向下运动，并与B物体发生连续碰撞（碰撞时间极短，忽略不计），每次碰后两物体交换速度。g取10 m/s2。求：
（1）A与B第一次碰后瞬间B的速率？
（2）从A开始运动到两物体第二次相碰经历多长时间？
（3）从A开始运动至第n次碰撞时A、B两物体通过的路程分别是多少？
解：A物体沿斜面下滑时：mAgsinθ-μAmAgcosθ=mAaA，所以aA=gsinθ-μAgcosθ
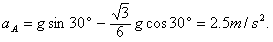
B物体沿斜面下滑时有：mBgsinθ-μBmBgcosθ=mBaB，所以aB=gsinθ-μBgcosθ
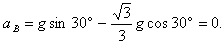
（1）由上面可知，撤去固定A、B的外力后，物体B恰好静止于斜面上，物体A将沿斜而向下做匀加速直线运动
A与B第一次碰撞前的速度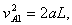
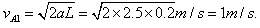
故A、B第一次碰后瞬间，B的速率v'B1=vA1=1 m/s
（2）从A开始运动到第一次碰撞用时：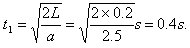
两物体相碰后，A物体的速度变为零，之后再做匀加速运动，而B物体将以v'B1=1 m/s的速度沿斜面向下做匀速直线运动
设再经t2时间相碰，则有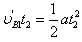
解之可得t2=0.8 s
故从A开始运动到两物体第二次相碰，共经历时间t=t1+t2=0.4 s+0.8 s=1.2 s
（3）碰后A、B交换速度，碰后B的速度均要比A的速度大1 m/s
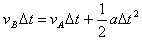，即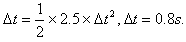
从第2次碰撞开始，每次A物体运动到与B物体碰撞前，速度增加量均为△v=a△t=2.5×0.8 m/s=2 m/s。由于碰后速度交换，因而碰后B物体的速度为：
第一次碰后：vB1=1 m/s
第二次碰后：vB2=2 m/s
第三次碰后：vB3=3 m/s
……
第n次碰后：vBn=n m/s
每段时间内，B物体都做匀速直线运动，则第n次碰时所运动的距离为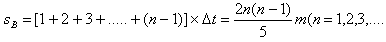
n-1)
A物体比B物体多运动L长度，则