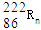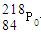问题
选择题
下面命题中正确的是( )
|
答案
A、由于直线过定点P0(x0,y0),
当直线斜率存在时,可用方程y-y0=k(x-x0)表示,
当直线斜率不存在时,方程是x=x0,故A不正确;
B、当x1=x2时,经过任意两个不同的点P1(x1,y1),P2(x2,y2)的直线方程是x=x1,
此时满足方程(y-y1)(x2-x1)=(x-x1)(y2-y1),
当x1≠x2时,经过任意两个不同的点P1(x1,y1),P2(x2,y2)的直线的斜率是
,y2-y1 x2-x1
则直线方程是y-y1=
(x-x1),整理得(y-y1)(x2-x1)=(x-x1)(y2-y1),故B正确;y2-y1 x2-x1
C、当直线斜率不存在时,不经过原点的直线方程是x=x0,不可以用方程
+x a
=1表示,y b
当直线的斜率存在时,可以用方程
+x a
=1表示,故C不正确;y b
D、当直线斜率不存在时,经过点A(0,b)的直线方程是x=0,不可以用方程y=kx+b表示,
当直线的斜率存在时,经过点A(0,b)的直线可以用方程y=kx+b表示,故D不正确.
故答案选B.

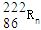 衰变成钋核
衰变成钋核 并放出一个粒子,其半衰期为3.8天.1g氡经过7.6天衰变掉的氡的质量,以及
并放出一个粒子,其半衰期为3.8天.1g氡经过7.6天衰变掉的氡的质量,以及