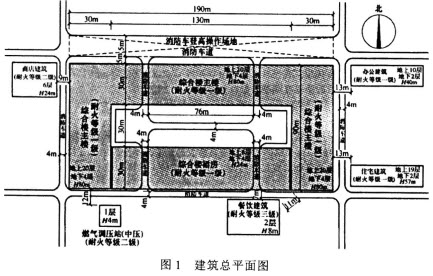
将质量均为m厚度不计的两物块A、B用轻质弹簧相连接,弹簧的劲度系数为k。第一次将B物块放在水平面上,A在弹簧弹力的作用下处于静止,如图(甲)所示,此时弹簧的弹性势能为Ep,现突然敲击A,使A在一瞬间获得向下的速度,在随后的过程中B物块恰能离开地面但不继续上升。第二次用手拿着A、B两物块,使得弹簧竖直并处于原长状态,此时物块B离地面的距离为H,如图(乙)所示,然后由静止同时释放A、B,B物块着地后速度立即变为0。若对于给定的弹簧,其弹性势能只跟弹簧的形变有关,求:
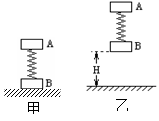
(1)第一次当B物块恰好离开地面时,A物块相对于自己静止时的初始位置升高的距离h
(2)第二次释放A、B后,A上升至弹簧恢复原长时的速度大小v1
(3)若弹簧的劲度系数k未知,但第一次敲击A后,A获得的速度大小v0已知。则第二次释放A、B后,B刚要离地时A的速度大小v2是多少?
(1)2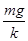 (2)
(2)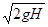 (3)
(3)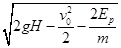
(1)第一次静止时,弹簧向上产生的弹力与A的重力平衡。
设弹簧的形变量(压缩)为△x1,有△x1=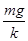 (2分)
(2分)
第一次当B刚要离地时弹簧产生向上的弹力与B的重力平衡
设弹簧的形变量(伸长)为△x2,有△x2=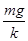 (2分) h=△x1+△x2=2
(2分) h=△x1+△x2=2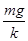 (2分)
(2分)
(2)第二次释放A、B后,A、B做自由落体运动,B着地后,A和弹簧相互作用至A上升到弹簧恢复原长过程中,弹簧对A做的总功为零 。
对A从开始下落至弹簧恢复原长过程,对A由动能定理有 mgH=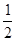 mv12 (3分)
mv12 (3分)
解得 v1=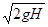 (3分)
(3分)
(3)第二次释放AB后,在B刚要离地时弹簧产生向上的弹力与B的重力平衡
设弹簧的形变量(伸长)为△x3,有△x3=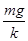 (2分)
(2分)
△x1=△x2=△x3
因此第一次静止时、第一次B刚要离地时和第二次B刚要离地时,弹簧的弹性势能都为Ep 在第一次A获得速度到B刚要离地时,对A和弹簧组成的系统,由机械能守恒有
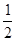 mv02+Ep=mg(△x1+△x2)+EP (2分)
mv02+Ep=mg(△x1+△x2)+EP (2分)
第二次释放后,对A和弹簧系统,从A上升至弹簧恢复原长到B刚要离地过程,由机械能守恒有 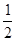 mv12=mg△x3+EP+
mv12=mg△x3+EP+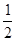 mv22 (2分)
mv22 (2分)
由以上解得v2=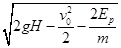 (2分)
(2分)