问题
计算题
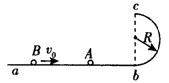
如图所示，abc是光滑的轨道，其中ab是水平的，bc是位于竖直平面内与ab相切的半圆，半径R=0.40 m。质量m=0.30 kg的小球A静止在水平轨道上，另一质量M=0.50 kg的小球B以v0=4 m/s的初速度与小球A发生碰撞。已知碰后小球A经过半圆的最高点c后落到轨道上距b点为L=1.2 m处，重力加速度g=10 m/s2。求：
(1)当A球经过半圆的最高点c时的速度大小；
(2)当A球经过半圆的最低点b时它对轨道的作用力；
(3)判断A，B碰撞是否是完全弹性碰撞。
答案
解：(1)设碰后小球A在半圆的最高点c时速度为vA'，球A随后离开c点做平抛运动，有
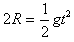，L=vA't
解得vA'=3 m/s
(2)设碰后小球A在半圆的最低点b时速度为vA，小球A从b点到c点由机械能守恒定律得
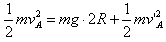
解得vA=5 m/s
在b点时，对A由牛顿运动定律可得：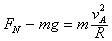
联立解得FN=21.75 N
根据牛顿第三定律，球对轨道的作用力FN'大小为21.75 N，方向竖直向下
(3)对碰撞过程，由动量守恒定律得Mv0=MvB+mvA
解得vB=1 m/s
由功能关系得，碰撞中产生的内能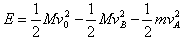
解得E=0
所以，球A，B的碰撞为完全弹性碰撞