在平面直角坐标系中描出四个点，如图所示：

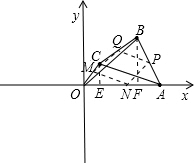
过C作CE⊥x轴，作BF⊥x轴，设M，N，P，Q分别为OC，OA，AB，BC的中点，

∵A（4，0），B（3，3），C（1，

3

），O（0，0），

∴CE=

3

，AE=OA-OE=4-1=3，

在Rt△ACE中，根据勾股定理得：AC=

CE2+AE2

=3

2

，

又BF=3，OF=3，

在Rt△OBF中，利用勾股定理得：OB=

BF2+OF2

=3

2

，

∴AC=OB，

又M为OC的中点，N为OA的中点，即MN为△OAC的中位线，

∴MN∥AC，MN=

1

2

AC，

同理PQ∥AC，PQ=

1

2

AC，NP=

1

2

OB，

∴PQ=MN，PQ∥MN，

∴四边形MNPQ为平行四边形，

又PQ=

1

2

AC，NP=

1

2

OB，且AC=OB，

∴PQ=NP，

则四边形MNPQ为菱形．

故选A