问题
问答题
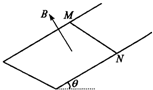
如图所示,足够长的光滑U形导体框架的宽度L=0.5m,电阻忽略不计,其所在平面与水平面成θ=37°角,磁感应强度B=0.8T的匀强磁场方向垂直于导体框平面,一根质量m=0.2kg,有效电阻R=2Ω的导体棒MN垂直跨放在U形框架上,导体棒与框架间的动摩擦因数为0.5,导体棒由静止开始沿框架下滑到刚开始匀速运动,通过导体棒截面的电量共为Q=2C.求:
(1)导体棒匀速运动的速度;
(2)导体棒从开始下滑到刚开始匀速运动这一过程中,导体棒的电阻消耗的电功.(sin 37°=0.6 cos 37°=0.8 g=10m/s2)
答案
(1)安培力F安=BIL,I=
,E=BLv,则F安=E R B2L2v R
导体棒匀速下滑时,由力平衡得
mgsin37°=F安+μmgcos37°
代入得mgsin37°=
+μmgcos37°,v=5m/sB2L2v R
(2)设导体棒由静止开始沿框架下滑到刚开始匀速运动下滑的距离为S,
通过导体棒截面的电量Q=
?△t,. I
=. I
,. E R
=. E
,得到△Φ △t
Q=
=△Φ R
得S=BLS R
=10mQR BL
根据能量守恒定律,得mgSsin37°=Q热+
mv2+μmgScos37°1 2
得Q热=mgSsin37°-
mv2-μmgScos37°=1.5J1 2
答:(1)导体棒匀速运动的速度为5m/s;
(2)导体棒从开始下滑到刚开始匀速运动这一过程中,导体棒的电阻消耗的电功为1.5J.
