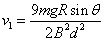问题
计算题
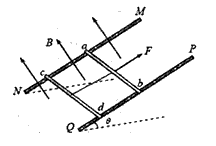
如图所示，两根足够长的平行光滑金属导轨MN、PQ间距为d,其电阻不计，两导轨所在的平面与水平面成θ角。质量分别为m和3m，电阻均为R的两金属棒ab、cd分别垂直导轨放置，每棒两端都与导轨始终有良好接触，两棒之间用一绝缘的细线相连，整个装置处在垂直于导轨平面向上的匀强磁场中，磁感应强度为B，给棒ab施加一平行于导轨向上的拉力作用，使两棒均保持静止。若在t=0时刻将细线烧断，此后保持拉力不变，重力加速度为g。
(1)细线烧断后，当ab棒加速度为a1时，求cd棒的加速度大小a2 (用a1表示)；
(2)求ab棒最终所能达到的最大速度。
答案
解：（1）烧断细线前拉力设为 ，则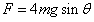
烧断细线后，对ab棒，设此时ab棒所受安培力的大小为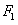
,由牛顿第二定律得：
同时，设cd棒此时所受安培力的大小为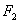
，由牛顿第二定律得： 
且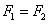
由以上各式解得：
；
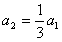（2）当ab棒和cd棒加速度为零时，速度均达最大, 设此时ab棒和cd棒的速度大小分别
由cd棒受力平衡：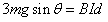
此时回路中总的电动势：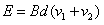
电路中电流：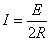
由动量守恒定律：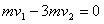
由以上各式解得：