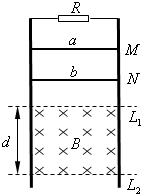
如图所示,电阻忽略不计的两根两平行光滑金属导轨竖直放置,其上端接一阻值为3Ω的电阻R.在水平虚线L1、L2间有一与导轨所在平面垂直的匀强磁场B,磁场区域的高度为d=0.5m.导体棒a的质量ma=0.2kg、电阻Ra=3Ω;导体棒b的质量mb=0.1kg、电阻Rb=6Ω,它们分别从图中M、N处同时由静止开始沿导轨向下滑动,且都能匀速穿过磁场区域,当b 刚穿出磁场时a正好进入磁场.(不计a、b之间的作用)求:
(1)在整个过程中,a棒和b棒分别克服安培力做了多少功?
(2)在b穿过磁场区域过程中,电阻R产生的电热;
(3)M点和N点距L1的高度分别为多少?
(1)因为两金属棒都是匀速穿过磁场的,所以安培力与重力等大,克服安培力做功分别为:Wa=magd=0.2×10×0.5J=1J
Wb=mbgd=0.1×10×0.5J=0.5J
(2)设b切割磁感线时,其上电流为I,则电阻R和a棒上电流均为
I,根据焦耳定律:Q=I2Rt得:1 2
Qb:Qa:QR=I2Rbt:(I/2)2Rat:(I/2)2Rt=8:1:1
由(1)知b棒穿过磁场过程产生的总电热为Q=0.5J
所以:QR=
Q=0.05J1 8+1+1
(3)b在磁场中匀速运动时:速度为υb,总电阻R1=7.5Ω.
b中的电流Ib=
①BLυb R1
由以上各式得:
=mbg②B2L2υb R1
a在磁场中匀速运动时:速度为va,总电阻R2=5Ω.
对a棒同理有:
=mag③B2L2υa R2
由②③式得,
=υb υa
④3 4
又:υa=υb+gt⑤d=υbt⑥
由④⑤⑥得:
=v 2a
,16gd 3
=3gdv 2b
所以:ha=
=v 2a 2g
d=8 3
×0.5m≈1.33m8 3
hb=
=1.5d=1.5×0.5m=0.75mv 2b 2g
答:(1)在整个过程中,a棒和b棒分别克服安培力做功1J和0.5J.
(2)在b穿过磁场区域过程中,电阻R产生的电热是0.05J;
(3)M点和N点距L1的高度分别为1.33J和0.75J.
