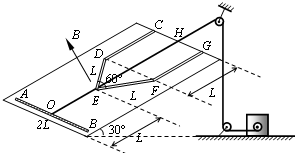
如图所示,在倾角为30°的光滑斜面上固定一光滑金属导轨CDEFG,图中OH∥CD∥FG,∠DEF=60°,CD=DE=EF=FG=OE=L;一根质量为m、长度为2L的导体棒AB在电机牵引下,以恒定速度v0沿OH方向从斜面底端滑上导轨并到达斜面顶端,O是AB棒的中点,AB⊥OH.金属导轨的CD、FG段电阻不计,DEF段与AB棒材料与横截面积均相同,单位长度的电阻均为r,整个斜面处在垂直斜面向上、磁感应强度为B的匀强磁场中.求:
(1)导体棒在导轨DEF上滑动时电路中电流的大小;
(2)导体棒运动到DF位置时AB两端的电压;
(3)将导体棒从底端拉到斜面顶端过程电机对杆做的功.
(1)设AB棒等效切割长度为l,则
感应电动势为E=Blv0
回路电阻为R=3lr
回路电流为I=
=E R Bv0 3r
(2)AB棒滑到DF处时
AB两端的电压UBA=UDA+UFD+UBF
UDA+UBF=BLv0
而UDF=
BLv0=2lr 3lr
BLv0 2 3
得UBA=UDA+UFD+UBF=
BLv05 3
(3)导体棒重力势能的增加量△EP=mg(2L+Lcos30°)sin30°=
mgL 4+ 3 4
AB棒在DEF上滑动时产生的电热Q1,数值上等于克服安培力做的功Q1=W安
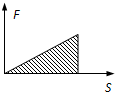
又因为F安∝S,如图,故 Q1=W安=
?0+F安max 2
L=3 2
B2L2v03 12r
AB棒在CDFG导轨上滑动时产生的电热Q2,电流恒定,电阻不变
则Q2=I2Rt=(
)2?3Lr?Bv0 3r
=L v0 B2L2v0 3r
得,电机做的功W=△EP+Q1+Q2=
(mgL+4+ 3 4
) B2L2v0 3r
答:(1)导体棒在导轨DEF上滑动时电路中电流的大小为流为
; Bv0 3r
(2)导体棒运动到DF位置时AB两端的电压为
BLv0;5 3
(3)将导体棒从底端拉到斜面顶端过程电机对杆做的功是
(mgL+4+ 3 4
).B2L2v0 3r
