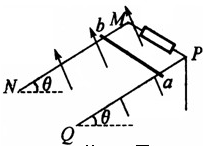
如图所示,两根足够长的直金属导轨MN、PQ平行放置在倾角为θ的绝缘斜面上,两导轨间距为L.M、P两点间接有阻值为R的电阻.一根质量为m的均匀直金属杆ab放在两导轨上,并与导轨垂直.整套装置处于匀强磁场中,磁场方向垂直于斜面向上.导轨和金属杆的电阻可忽路.让金属杆ab沿导轨由静止开始下滑,经过足够长的时间后,金属杆达到最大速度vm,在这个过程中,电阻R上产生的热量为Q.导轨和金属杆接触良好,它们之间的动摩擦因数为μ且μ<tanθ.已知重力加速度为g.
(1)求磁感应强度的大小;
(2)金属杆在加速下滑过程中,当速度达到v1(v1<vm)时,求此时杆的加速度大小;
(3)求金属杆从静止开始至达到最大速度的过程中下降的高度.
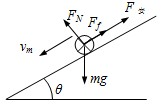
(1)当ab匀速运动时,金属杆的受力图如图所示(从前向后看的视图):图中Ff为滑动摩擦力,FN为斜面支持力,F安为感应电流的安培力,mg为导体棒的重力.这时导体棒匀速直线运动,其所受的合力为零,则有:
mgsinθ=Ff+F安
FN=mgcosθ,
由滑动摩擦力公式:Ff=μFN,
由安培力公式F安=BIL,由欧姆定律I=
,由法拉第电磁感应定律得E=BLvm,得F安=E R B2L2vm R
解得:B=mgR(sinθ-μcosθ) L2vm
(2)当导体棒的速度为v1时,由牛顿第二定律得:mgsinθ-μmgcosθ-BI'L=ma,
其中I'为速度时v1时导体棒中的感应电流,I'=
,BLv1 R
代入上式解得加速度 a=g(sinθ-μcosθ)(1-
)v1 vm
(3)由能量守恒知,导体棒减少的重力势能,转化为动能、内能和电能,电能通过电阻R又转化为热量.所以满足:
mgh=
m1 2
+W′+Q,其中W'为克服摩擦力做的功,v 2m
W′=μFN?
,FN=mgcosθ,h sinθ
解得金属棒下降的高度为 h=m
+2Qv 2m mg(1-μcotθ)
答:
(1)磁感应强度的大小为
;mgR(sinθ-μcosθ) L2vm
(2)金属杆在加速下滑过程中,当速度达到v1(v1<vm)时,此时杆的加速度大小为g(sinθ-μcosθ)(1-
);v1 vm
(3)金属杆从静止开始至达到最大速度的过程中下降的高度为
.m
+2Qv 2m mg(1-μcotθ)
