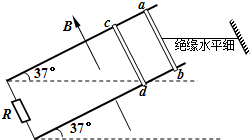
如图所示,相距0.5m足够长的两根光滑导轨与水平面成37°角,导轨电阻不计,下端连接阻值为2Ω的电阻R,导轨处在磁感应强度B=2T的匀强磁场中,磁场方向垂直导轨平面斜向上.ab、cd为水平金属棒且与导轨接触良好,它们的质量均为0.5kg、电阻均为2Ω.ab棒与一绝缘水平细绳相连处于静止状态,现让cd棒从静止开始下滑,直至与ab相连的细绳刚好被拉断,在此过程中电阻R上产生的热量为0.5J,已知细线能承受的最大拉力为5N.求细绳被拉断时:(g=10m/s2,sin37°=0.6)
(1)ab棒中的电流大小;
(2)cd棒的速度大小;
(3)cd棒下滑的距离.
(1)细绳被拉断瞬时,对ab棒受力分析得,Fm cos37°=mgsin37°+BIabL
代入数据解得,Iab=1A
(2)分析电路可知,Iab=IR,Icd=Iab+IR=2A
根据闭合欧姆定可得,BLv=Icd(Rcd+
)RabR Rab+R
联立可得,v=6 m/s
(3)金属棒cd从静止开始运动直至细绳刚好被拉断的过程中,由焦耳定律得,Qab=
t=I2Rabt,QR=U2 Rab
t=I2RtU2 R
代入数据解得,Qab=QR=0.5J,Qcd=(2I)2Rcdt=4I2Rabt=2J
由能量守恒得,mgssin37°=
mv2+Qab+Qcd+QR1 2
解得s=4m
