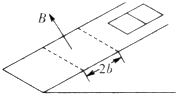
如图所示,有一个倾角为θ的足够长的斜面,沿着斜面有一宽度为2b的匀强磁场,磁感应强度为B,方向垂直斜面向外,磁场的边界与底边平行.现有一质量为m的“日”字形导线框,框上两个小正方形的边长均为b.其中三条平行边和斜面底边及磁场边界平行,电阻均为R,其余两条长平行边不计电阻.现将导线框由静止开始释放,整个框和斜面的动摩擦因数为μ(μ<tanθ),当它刚滑进磁场时恰好做匀速直线运动.问:
(1)导线框从静止开始到进入磁场时所滑过的距离s;
(2)通过计算说明导线框能否匀速通过整个磁场;
(3)导线框从静止开始到全部离开磁场所产生的焦耳热Q.
(1)线框刚进磁场时匀速直线运动,则有 mgsinθ=μmgcosθ+F安
又由F安=BIb,I=
,E=Bbv,E R+ R 2
联立可得:v=3mgR(sinθ-μcosθ) 2B2b2
线框未进磁场时,加速度为a=
=gsinθ-μgcosθmgsinθ-μmgcosθ m
则得 s=v2 2a
代入可得:s=9m2R2g(sinθ-μcosθ) 8B4b4
(2)能,在穿越过程中,当只有一条边在磁场中时有E=Bbv,I=
,F安=BIb都不变,仍然有mgsinθ=μmgcosθ+F安,因而能匀速滑动,而当有两条边在磁场中时,把它们看成整体,则E=Bbv,I=E R+ R 2
,F安=BIb不变,仍有mgsinθ=μmgcosθ+F安,因而能匀速滑动,综上所述能匀速地通过整个磁场.E
+RR 2
(3)对于线框穿越磁场的整个过程,由能量守恒得:mg(4bsinθ)=Q+μ(mgcosθ)4b,
解得 Q=4mgb(sinθ-μcosθ).
答:
(1)导线框从静止开始到进入磁场时所滑过的距离s为
;9m2R2g(sinθ-μcosθ) 8B4b4
(2)通过计算说明导线框能匀速通过整个磁场;
(3)导线框从静止开始到全部离开磁场所产生的焦耳热Q为4mgb(sinθ-μcosθ).
