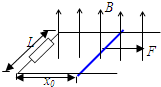
如图所示,水平导轨间距为L左端接有阻值为R的定值电阻,在距左端x0处放置一根质量为m、电阻为r的导体棒,导体棒与导轨间无摩擦且始终保持良好接触,导轨的电阻可忽略,整个装置处在竖直向上的匀强磁场中,问:在下列各种情况下,作用在导体棒上的水平拉力F的大小应如何?
(1)磁感应强度为B=B0保持恒定,导体棒以速度v向右做匀速直线运动;
(2)磁感应强度为B=B0+kt随时间t均匀增强,导体棒保持静止;
(3)磁感应强度为B=B0保持恒定,导体棒由静止始以加速度a向右做匀加速直线运动;
(4)磁感应强度为B=B0+kt随时间t均匀增强,导体棒以速度v向右做匀速直线运动.
(1)导体棒切割磁感线运动产生感应电动势E=BLv…①
感应电流为 I=
…②E R+r
根据平衡条件得:F=B0IL=
…③
L2vB 20 R+r
(2)根据法拉第定律得回路中产生的感应电动势 E=
=△φ △t
Lx0…④△B △t
由B=B0+kt知
=k…⑤△B △t
得 E=kLx0…⑥
则得 F=BiL=
=BLv R+r
(B0+kt)…⑦kx0L2 R+r
(3)t时刻导体棒的速度为 v=at…⑧
根据牛顿第二定律得 F-BIL=ma…⑨
则 F=BIL+ma=
at+ma…⑩
L2B 20 R+r
(4)回路中既有动生电动势,又有感生电动势,根据楞次定律判断可知两个电动势方向相同,则回路中总的感应电动势为
E=
=BLv+kL(x0+vt)=(B0+kt)Lv+kL(x0+vt)…(11)△φ △t
则 F=BIL=
=BLE R+r
…(12)(B0+kt)[(B0+kt)v+k(x0+vt)]L2 R+r
答:
(1)磁感应强度为B=B0保持恒定,导体棒以速度v向右做匀速直线运动时,拉力为
.
L2vB 20 R+r
(2)磁感应强度为B=B0+kt随时间t均匀增强,导体棒保持静止时,拉力为
(B0+kt);kx0L2 R+r
(3)磁感应强度为B=B0保持恒定,导体棒由静止始以加速度a向右做匀加速直线运动时拉力为
at+ma.
L2B 20 R+r
(4)磁感应强度为B=B0+kt随时间t均匀增强,导体棒以速度v向右做匀速直线运动时拉力为
.(B0+kt)[(B0+kt)v+k(x0+vt)]L2 R+r