相距L=0.8m的足够长金属导轨的左侧为水平轨道,右侧为倾角37°的倾斜轨道,金属棒ab和金属棒cd分别水平地放在两侧的轨道上,如图(a)所示,两金属棒的质量均为1.0kg.水平轨道位于竖直向下的匀强磁场中,倾斜轨道位于沿斜面向下的匀强磁场中,两个磁场的磁感应强度大小相等.ab、cd棒与轨道间的动摩擦因数为μ=0.5,两棒的总电阻为R=1.5Ω,导轨电阻不计.ab棒在水平向左、大小按图(b)所示规律变化的外力F作用下,由静止开始沿水平轨道做匀加速运动,同时cd棒也由静止释放.(sin37°=0.6,cos37°=0.8,重力加速度g取10m/s2)
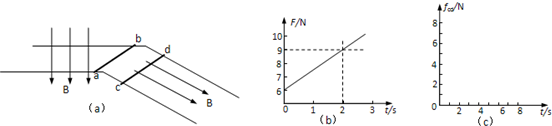
(1)求两个磁场的磁感应强度B的大小和ab棒的加速度a1的大小;
(2)已知在2s内外力F做功为18J,求这一过程中两金属棒产生的总焦耳热;
(3)写出cd棒运动的加速度a2(m/s2)随时间t(s)变化的函数式a2(t),并求出cd棒达到最大速度所需的时间t0;
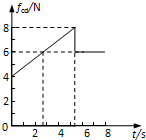
(4)请在图(c)中画出cd棒受到的摩擦力fcd随时间变化的图象.
(1)根据牛顿第二定律得:
ab棒:F-μmg-FA=m1a1
其中安培力FA=BIL=B2L2a1t R
对ab棒有:m1a1=F-μmg-FA,
结合图象的信息,将t=0时,F=6N、FA=0 代入,可求得a1=1m/s2
a1为定值,则
=1.5,B2L2a1 R
将L=0.8m、R=1.5Ω、a1=1m/s2代入上式,可求得B=1.875T
(2)2s末,ab棒的速度υt=a1t=2m/s,位移s=
a1t2=2m1 2
对ab棒,由能量守恒得
WF=
mυt2+μm1gs+Q,1 2
可解得Q=6J
(3)对cd棒有m2gsin37°-μ(m2gcos37°+FA)=m2a2,
其中FA=BIL=B2L2a1t R
可得a2=2-0.75t
a2=0时cd棒的速度最大,此时t=2.67s
(4)cd棒受到的摩擦力fcd=μ(m2gcos37°+FA)=4+0.75t
作出fcd随时间变化的图象如图所示.
答:
(1)两个磁场的磁感应强度B的大小为1.875T,ab棒的加速度a1的大小为1m/s2;
(2)这一过程中两金属棒产生的总焦耳热是6J;
(3)cd棒运动的加速度a2(m/s2)随时间t(s)变化的函数式a2(t)为a2=2-0.75t,cd棒达到最大速度所需的时间t0为t=2.67s.
(4)在图(c)中画出cd棒受到的摩擦力fcd随时间变化的图象如图所示.
