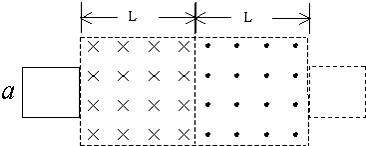
如图所示,在光滑的水平面上有两个方向相反的匀强磁场垂直穿过,磁场的宽度均为L,磁感应强度大小均为B,水平面上放有一正方形金属线框,其边长为a(a<L),电阻为R.
(1)若线框以速度v从磁场区左侧匀速向右穿过该磁场区域到达磁场区右侧的过程中,求外力所做的功.
(2)若线框从磁场区左侧以水平向右的某个初速度进入磁场,刚好能从磁场区右侧全部出来,求线框在进入磁场和离开磁场的过程中产生的热量之比.
(1)线圈进入磁场的过程中,安培力做功
W1=F1a=(I1aB)a=(
aB)a=Bav R B2a3v R
线圈从左侧磁场进入右侧磁场的过程中,
安培力做功W2=F2a=(2I2aB)a=(2
aB)a=2Bav R 4B2a3v R
线圈离开磁场的过程中,安培力做功
W3=F3a=(I3aB)a=(
aB)a=Bav R B2a3v R
整个过程中外力做功等于安培力做的总功
W=W1+W2+W3=6B2a3v R
(2)设线圈进入磁场前的初速度为v0,在左侧磁场中运动的速度为v1,线圈在右侧磁场中运动的速度为v2,线圈的质量为m
线圈在进入磁场过程中,根据动量定理得:
-
t1=-(. F1
aB)t1=mv1-mv0. I1
又感应电荷量q1=
t1.. I1
即-q1aB=mv1-mv0 ①
线圈从左侧磁场进入右侧磁场的过程中,同理可得:
-2F2t2=-2(
aB)t2=mv2-mv1. I2
即-2q2aB=mv2-mv1 ②
线圈离开磁场的过程中,同理可得:
-
t3=-(. F3
aB)t3=-mv2. I3
即-q3aB=0-mv2 ③
又感应电荷量q1=
,q2=△Φ1 R
,q3=△Φ2 R △Φ3 R
其中△Φ1=△Φ2=Ba2,△Φ3=2Ba2,
所以q2=2q1,q3=q1
由①②③式解得v1=
v0,v2=5 6
v01 6
所以
=Q1 Q2
=
m1 2
-v 20
m1 2 v 21
m1 2
-0v 22
=
-v 20 v 21 v 22 11 1
答:
(1)外力所做的功为
.6B2a3v R
(2)线框在进入磁场和离开磁场的过程中产生的热量之比为11:1.
