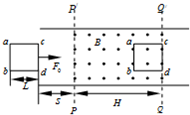
如图所示,光滑水平面上有正方形金属线框abcd,边长为L、电阻为R、质量为m.虚线PP’和QQ’之间有一竖直向上的匀强磁场,磁感应强度为B,宽度为H,且H>L.线框在恒力F0作用下由静止开始向磁场区域运动,cd边运动S后进入磁场,ab边进入磁场前某时刻,线框已经达到平衡状态.当cd边到达QQ’时,撤去恒力F0,重新施加外力F,使得线框做加速度大小为F0/m的匀减速运动,最终离开磁场.
(1)cd边刚进入磁场时cd两端的电势差;
(2)cd边从进入磁场到QQ’这个过程中安培力做的总功;
(3)写出线框离开磁场的过程中,F随时间t变化的关系式.
(1)线圈进入磁场前线圈做匀加速运动,牛顿第二定律和速度公式加速度为 a=F0 m
cd刚进入磁场时速度为 v=at
而线圈通过的位移s=
at21 2
解得,v=2F0s m
cd边刚进入磁场时产生的感应电动势 E=BLv
此时cd边的电势差U=
E3 4
联立以上各式得 U=
BL3 4
.2F0s m
(2)进入磁场后达到平衡时,设此时速度为v1,则有F0=BIL=B2L2v1 R
得v1=F0R B2L2
根据动能定理得 F0(L+s)+W安=
m1 2 v 21
W安=-F0(L+s)+m
R2F 20 2B4L4
(3)平衡后到开始离开磁场时,设线圈开始离开磁场时速度为v2
F0(H-L)=
mv22-1 2
mv121 2
解得,v2=
+
R2F 20 B4L4 2F0(H-L) m
此时的安培力
>maB2L2v2 R
所以,离开磁场
-F=maB2L2v R
而v=v2-at,
代入v2 得F=B2L2 R
-F0-
+
R2F 20 B4L4 2F0(H-L) m
tB2L2F0 mR
答:
(1)cd边刚进入磁场时cd两端的电势差为
BL3 4
.;2F0s m
(2)cd边从进入磁场到QQ’这个过程中安培力做的总功为-F0(L+s)+
;m
R2F 20 2B4L4
(3)写出线框离开磁场的过程中,F随时间t变化的关系式为B2L2 R
-F0-
+
R2F 20 B4L4 2F0(H-L) m
t.B2L2F0 mR
