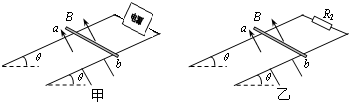
两足够长的平行金属导轨间的距离为L,导轨光滑且电阻不计,导轨所在的平面与水平面夹角为θ.在导轨所在平面内,分布磁感应强度为B、方向垂直于导轨所在平面的匀强磁场.把一个质量为m的导体棒ab放在金属导轨上,在外力作用下保持静止,导体棒与金属导轨垂直、且接触良好,导体棒与金属导轨接触的两点间的电阻为R1.完成下列问题:
(1)如图甲,金属导轨的一端接一个内阻为r的导体棒.撤去外力后导体棒仍能静止.求导体棒上的电流方向和电源电动势大小?
(2)如图乙,金属导轨的一端接一个阻值为R2的定值电阻,让导体棒由静止开始下滑,求导体棒所能达到的最大速度?
(3)在(2)问中当导体棒下滑高度为h速度刚好达最大,求这一过程,导体棒上产生的热量和通过电阻R2电量?
(1)由左手定则可得:b指向a
回路中的电流为 I= ①
导体棒受到的安培力为 F安=BIL ②
对导体棒受力分析知 F安=mgsinθ ③
联立上面三式解得:E= ④
(2)当ab杆速度为v时,感应电动势 E=BLv,此时电路中电流 I== ⑤
当 =mgsinθ时,ab杆达到最大速度 vm
vm= ⑥
(3)由能的转化和守恒定律可得:mgh=Q总+m ⑦
导体棒上产生的热量 Q棒=Q总 ⑧
联立⑥⑦⑧得:Q棒=(mgh-) ⑨
由=,=,q=•△t,△Φ=BL•
联立得通过电阻R2电量 q= ⑩
答:
(1)导体棒上的电流方向为和b指向a,电源电动势大小为.
(2)导体棒所能达到的最大速度为.
(3)导体棒上产生的热量为(mgh-),通过电阻R2电量为.