如图甲所示,质量为m=50g,长l=10cm的铜棒,用长度亦为l的两根轻软导线水平悬吊在竖直向上的匀强磁场中,磁感应强度B=1/3T.未通电时,轻线在竖直方向,通入恒定电流后,棒向外偏转的最大角度θ=37°,求此棒中恒定电流的大小.
同学甲的解法如下:对铜棒进行受力分析,通电时导线向外偏转,说明安培力方向垂直电流和磁场方向向外,受力如图乙所示(侧视图).
当最大偏转角θ=37°时,棒受力平衡,有:tanθ=
=F mg BIl mg
∴I=
=mgtanθ Bl
A=11.25A0.05×10× 3 4
×0.011 3
同学乙的解法如下:铜棒向外偏转过程中,导线拉力不做功,如图丙所示.
F做功为:WF=FS1=BIl•lsin37°
重力做功为:WG=-mgS2=-mgl(1-cos37°)
由动能定理得:BIl2sin37-mgl(1-cos37°)=0
∴I=
=mg(1-cos°) BIsin37°
A=5A0.05×10×(1-0.8)
×0.1×0.61 3
请你判断,他们的解法哪个正确?错误的请指出错在哪里.
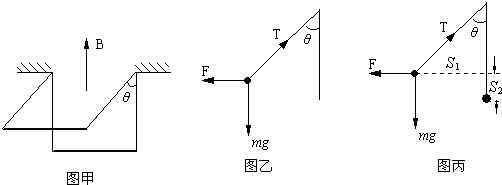
乙同学的解法正确,甲同学的错误.
错误原因:认为物体速度为零时,一定处于平衡状态,或者认为偏角最大的是平衡位置.
因为在最大偏角处,铜棒受到重力mg、安培力F和细线的拉力T,虽然铜棒的速度为零,但受力并不平衡,类似于单摆,三个力的合力沿圆弧的切线方向.所以甲同学解答不正确.
由于安培力F是恒力,可以根据功的公式求其做功,F做功为:WF=FS1=BIl•lsin37°,对于偏转过程,对铜棒运用动能定理列式是可以求出I的.
