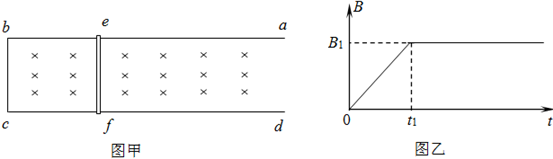
如图甲所示,固定于水平桌面上的金属导轨abcd足够长,金属棒ef搁在导轨上,可无摩擦地滑动,此时bcfe构成一个边长为l的正方形.金属棒的电阻为r,其余部分的电阻不计.在t=0的时刻,导轨间加一竖直向下的磁场,磁感应强度随时间的变化如图乙所示.为使金属棒ef在0-t1保持静止,在金属棒ef上施加一水平拉力F,从t1时刻起保持此时的水平拉力F不变,金属棒ef在导轨上运动了s后刚好达到最大速度,求:
(1)在t=时刻该水平拉力F的大小和方向;
(2)金属棒ef在导轨上运动的最大速度;
(3)从t=0开始到金属棒ef达到最大速度的过程中,金属棒ef中产生的热量.
(1)时刻,感应电动势E=S=,
导体棒受到的安培力F安=•I•l=••l=,
由楞次定律可知,感应电流从f流向e,由左手定则可知,导体棒受到的安培力向左;
由平衡条件可知,此时水平拉力F=,方向水平向右;
(2)导体棒切割磁感线产生感应电动势,
当金属棒的速度最大时,感应电动势E′=B1lvm,
此时导体棒受到的安培力F安′=B1••l,
此时水平拉力F′=2×=,
当安培力与拉力合力为零时,导体棒做匀速直线运动,此时速度最大,
即:F′=F安′,=B1••l;
解得,导体棒的最大速度:vm=;
(3)金属棒静止时的感应电流:=,
产生的焦耳热:Q1=rt1=,
金属棒从开始运动到最大速度阶段,
由能量守恒定律,得:Q2=Fs-m=•s-m()2=-,
全过程产生的焦耳热Q=Q1+Q2=-;
答:(1)在t=时刻该水平拉力F的大小为,方向水平向右;
(2)金属棒ef在导轨上运动的最大速度是;
(3)从t=0开始到金属棒ef达到最大速度的过程中,金属棒ef中产生的热量是-.

