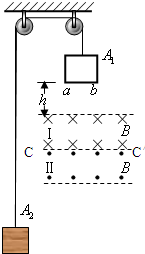
如图所示,轻绳绕过轻滑轮连接着边长为L的正方形导线框A1和物块A2,线框A1的电阻为R,质量为M,物块A2的质量为m(M>m),两匀强磁场区域Ⅰ、Ⅱ的高度也为L,磁感应强度均为B,方向水平与线框垂直.线框ab边磁场边界高度为h,开始时各段绳都处于伸直状态,把它们由静止释放,ab边刚穿过两磁场的分界线cc′进入磁场Ⅱ时线框做匀速运动.求:
(1)ab边进入磁场Ⅰ时线框A1的速度v1;
(2)ab边进入磁场Ⅱ后线框A1所受重力的功率P;
(3)从ab边进入磁场Ⅱ到ab边穿出磁场Ⅱ的过程中,线框中产生的焦耳热Q.
(1)线框进入磁场前的运动过程,应用系统机械能守恒得
(Mg-mg)h=
(M+m)1 2 v 21
得:v1=2(M-m)gh M+m
(2)设ab边进入磁场Ⅱ时线框匀速运动的速度为v2,此时线框中产生的感应电动势大小为E=2BLv2,感应电流为I=E R
线框的左右受到的安培力平衡,而上下两边所受的安培力的合力为F=2BIL,则得 F=2•2B2L2v2 R
根据平衡条件有
mg+2•
=Mg2B2L2v2 R
解得,v2=(M-m)gR 4B2L2
所以线框A1所受重力的功率P为:P=Mgv2=M(M-m)g2R 4B2L2
(3)从ab边进入磁场Ⅱ到ab边穿出磁场Ⅱ的过程中,线框做匀速直线运动,系统的重力势能减小转化为内能,由能量守恒定律得
Q=(M-m)gL
答:
(1)ab边进入磁场Ⅰ时线框A1的速度v1是
.2(M-m)gh M+m
(2)ab边进入磁场Ⅱ后线框A1所受重力的功率P是
;M(M-m)g2R 4B2L2
(3)从ab边进入磁场Ⅱ到ab边穿出磁场Ⅱ的过程中,线框中产生的焦耳热Q是(M-m)gL.
