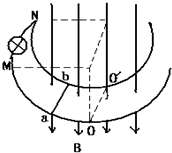
如图所示,半径为r、电阻不计的两个半圆形光滑导轨并列竖直放置,在轨道左上方端点M、N间接有阻值为R的小灯泡,整个轨道处在磁感应强度为B的匀强磁场中,两导轨间距为L,现有一质量为m,电阻也是R的金属棒ab从M、N处由静止释放,经一定时间到达导轨最低点0、0ˊ,此时速度为υ.
(1)指出金属棒ab从M、N到0、0ˊ的过程中,通过小灯泡的电流方向和金属棒ab的速度大小变化情况;
(2)求金属棒ab到达0、0ˊ时,整个电路的瞬时电功率;
(3)求金属棒ab从M、N到0、0ˊ的过程中,小灯泡上产生的热量.
(1)由右手定则可判:电流方向由N到M,
ab棒由静止开始作圆周运动,速度先增大,当安培力和重力的合力方向指向圆心时速度达到最大,之后开始做减速运动,故ab棒的速度先变大后变小.
(2)在最低点ab棒切割磁力线产生的:E=BLυ ①
由闭合电路欧姆定律得:I=
②E 2R
瞬时功率:P=EI ③
①②③联立得:P=B2L2v2 2R
(3)在ab棒下滑的过程中设小灯泡上产生的热量为Q,则整个电路上产生的热量为2Q,
由能量守恒定律得:mgr=
mv2+2Q 1 2
解得:Q=m(2gr-v2) 4
(1)通过小灯泡的电流方向由N到M,ab棒的速度先变大后变小.
(2)整个电路的瞬时电功率为
;B2L2v2 2R
(3)小灯泡上产生的热量Q=
.m(2gr-v2) 4
