问题
解答题
在△ABC中，AB=AC，AC边上的中线BD把三角形的周长分为12cm和15cm两部分，求三角形各边的长。
答案
解：设AB=x（cm），则AD=DC=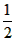
x（cm）．
（1）若AB+AD=12，即x+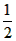
x=12． 所以x=8。
即AB=AC=8cm，则DC=4cm， 故BC=15-4=11cm， 此时AB+AC>BC，
所以三边长分别为8cm，8cm，11cm。
（2）若AB+AD=15，即x+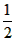
x=15，所以x=10，则DC=5cm， 故BC=12-5=7cm，
显然此时三角形存在， 所以三边长分别为10cm，10cm，7cm。
综上所述，此三角形的三边长分 别为： 8cm，8cm，11cm或10cm，10cm，7cm．