问题
问答题
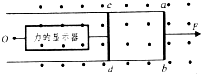
如图所示,在光滑的水平桌面上,放置一两边平行的质量为M,宽为L的足够长的“U”开金属框架,其框架平面与桌面平行.其ab部分的电阻为R,框架其它部分电阻不计.垂直框架两边放一质量为m、电阻为R的金属棒cd,它们之间的动摩擦因数为μ,且接触始终良好.cd棒通过不可伸长的细线与一个固定在O点力的显示器相连,始终处于静止状态.现在让框架由静止开始在水平恒定拉力F的作用下(F是未知数),向右做加速运动,设最大静摩擦力和滑动摩擦力相等.最终框架匀速运动时力的显示器的读数为2μmg.已知框架位于竖直向上足够大的匀强磁场中,磁感应强度为B.求
(1)框架和棒刚运动的瞬间,框架的加速度为多大?
(2)框架最后做匀速运动时的速度多大?
答案
(1)对框架、cd棒受力分析如图:当框架匀速运动时,
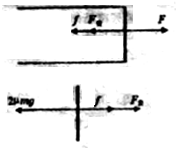
对框架有:F=f+F安,
对棒cd有:2μmg=f+F安,
则得F=2μmg
框架和棒刚运动的瞬间,对框架,由牛顿纴第二定律得
F-2μmg=Ma
解得 a=μmg M
(2)设框架最后做匀速运动时的速度大小为v,则感应电动势为E=BLv
回路中感应电流为 I=E R+R
对框架,由力的平衡得:F=BIL+μmg
联立以上各式得到:v=2μmgR B2L2
答:
(1)框架和棒刚运动的瞬间,框架的加速度为
.μmg M
(2)框架最后做匀速运动时的速度为
.2μmgR B2L2
