如图甲所示,两根相距为L的金属轨道固定于水平面上,导轨电阻不计,一根质量为m、长为L、电阻为R的金属棒两端放于导轨上,导轨与金属棒间的动摩擦因数为µ,棒与导轨的接触电阻不计.导轨左端连有阻值为2R的电阻,在电阻两端接有电压传感器并与计算机相连.有n段竖直向下的宽度为a间距为b的匀强磁场(a>b),磁感强度为B、金属棒初始位于OO′处,与第一段磁场相距2a.
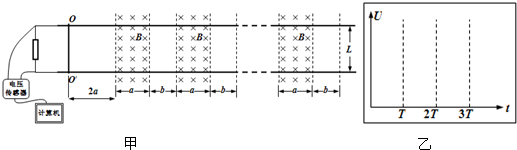
(1)若金属棒有向右的初速度v0,为使金属棒保持v0一直向右穿过各磁场,需对金属棒施加一个水平向右的拉力,求金属棒进入磁场前拉力F1的大小和进入磁场后拉力F2的大小;
(2)在(1)的情况下,求金属棒从OO′开始运动到刚离开第n段磁场过程中,拉力所做的功;
(3)若金属棒初速为零,现对棒施以水平向右的恒定拉力F,使棒穿过各段磁场,发现计算机显示出的电压随时间以固定的周期做周期性变化,在给定的坐标图乙中定性地画出计算机显示的图象(从金属棒进入第一段磁场开始计时).
(4)在(3)的情况下,求整个过程导轨左端电阻上产生的热量,以及金属棒从第n段磁场穿出时的速度.
(1)金属棒进入磁场前,F1=f=μN=μmg
金属棒在磁场中运动时,F2=f+F安=f+BIL
又I=
=E 2R+R
,BLv0 3R
联立得 F2=μmg+B2L2v0 3R
(2)在非磁场区域外力F1所做的功为 W1=F1[2a+(n-1)b]=μmg[2a+(n-1)b]
在磁场区域外力F2所做的功为 W2=F2×na=(μmg+
)naB2L2v0 3R
在此过程拉力所做的总功 W=W1+W2=μmg[(n+2)a+(n-1)b]+nB2L2avo 3R
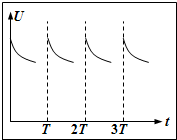
(3)要使棒进入各磁场的速度都相同,金属棒在无磁场区域做加速运动,在磁场区域做减速运动,则穿过各段磁场时,感应电动势减小,路端电压减小,而且速度减小时,安培力减小,加速度减小,则路端电压减小变化慢,电压图象的斜率减小,可作出电压图象如图.
(4)进入各磁场时的速度均相同,等于从OO´运动2a位移时的速度,根据动能定理得
(F-μmg)×2a=
mv′21 2
每经过一段磁场产生的电能相同,设为E电,根据动能定理,有
Fa-μmga-E电=
mv2-1 2
mv′21 2
所以
E电=Fa-μmga-
mv2+1 2
mv′21 2 =Fa-μmga-(F-μmg)(2a-b)+(F-μmg)×2a =(F-μmg)(a+b)
Q=
×2R=nE电 3R
n(F-μmg)(a+b),2 3
解得 v=(F-μmg)(4a-2b) m
答:(1)金属棒进入磁场前拉力F1的大小为μmg,进入磁场后拉力F2的大小为μmg+
;B2L2v0 3R
(2)金属棒从OO′开始运动到刚离开第n段磁场过程中,拉力所做的功为μmg[(n+2)a+(n-1)b]+
;nB2L2av0 3R
(3)电压图象如图;
(4)整个过程导轨左端电阻上产生的热量为
n(F-μmg)(a+b),金属棒从第n段磁场穿出时的速度为2 3
.(F-μmg)(4a-2b) m
