问题
问答题
一个质量m=0.1kg的正方形金属框总电阻R=0.5Ω,金属框从表面绝缘且光滑的斜面顶端(金属框上端与AA′重合)由静止开始沿斜面下滑,下滑过程中穿过一段边界与斜面底边BB′平行、宽度与线框边长相同的匀强磁场后滑至斜面底端(金属线框下边与BB′重合),设金属框在下滑过程中的速度为v,与其对应的位移为s,整个运动过程的v2-s图象如图所示,已知匀强磁场方向垂直斜面向上,取g=10m/s2
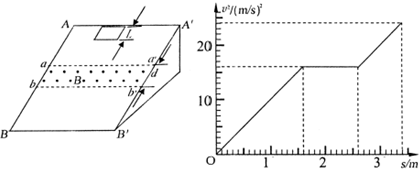
(1)根据v2-s图象所提供的信息,计算出斜面倾角θ和磁场宽度d.
(2)匀强磁场的磁感应强度多大?
答案
(1)据v2-s图象知,当线框进入磁场时:v2=16(m/s)2,s=1.6m
由v2=2as得:a=
=5m/s2.v2 2s
对线框,由牛顿第二定律得:mgsinθ=ma
解得:θ=30°
磁场的宽厚d=
2m=0.5m2.6-1.6 2
(2)由图线知线框穿过磁场的过程中匀速运动,且v=
m/s=4m/s16
由平衡条件得:F磁=mgsinθ
又F磁=BId=Bd•
=E R (Bd)2v R
由上两式解得:B=0.5T
答:
(1)斜面倾角θ为30°,磁场宽度d是0.5m.
(2)匀强磁场的磁感应强度是0.5T.
