在竖直面内有两平行金属导轨AB、CD,间距为L,金属棒ab可在导轨上无摩擦地滑动.棒与导轨垂直,并接触良好.它们的电阻均可不计.导轨之间有垂直纸面向外的匀强磁场,磁感强度为B.导轨右边与电路连接.电路中的三个定值电阻R1、R2、R3阻值分别为2R、R和0.5R.在BD间接有一水平放置的平行板电容器C,极板间距离为d.
(1)当ab以速度v0匀速向左运动时,电容器中质量为m的带电微粒恰好静止.试判断微粒的带电性质,及带电量的大小.
(2)当ab棒以某一速度沿导轨匀速运动时,发现带电微粒从两极板中间由静止开始向下运动,历时t=2×10-2 s到达下极板,已知电容器两极板间距离d=6×10-3m,求ab棒的速度大小和方向.(g=10m/s2)
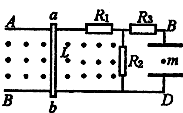
(1)棒匀速向左运动,感应电流为顺时针方向,电容器上板带正电,板间场强向下.
∵微粒受力平衡,电场力向上,场强方向向下.
∴微粒带负电.
设微粒带电量大小为q,由平衡条件知:mg=q
…①UC d
对R1、R2和金属棒构成的回路,由欧姆定律可得
I=
…②E 3R
UC=IR2=IR…③
由法拉第电磁感应定律可得 E=BLv0…④
由以上各式求得 q=
…⑤3mgd BLv0
(2)因带电微粒从极板中间开始向下作初速度为零的匀加速运动,
由运动学公式得:
d=1 2
at2…⑥1 2
得 a=15m/s2=
g>g…⑦3 2
可见带电微粒受到的电场力向下,所以ab棒应向右运动,设此时极板间电压为UC′,由牛顿第二定律,得
mg+q
=m•UC′ d
g…⑧3 2
出⑤和⑧得 UC′=
BLv01 6
设棒ab运动速度为vx,则电动势E′=Blvx,由欧姆定律得:
UC′=I′R2=
•R=BLvx 3R
BLvx=1 3
nlv01 6
∴vx=
v0.即棒运动速度大小应为原来速度的一半,即为1 2
v0.1 2
答:
(1)微粒的带负电,带电量的大小为
.3mgd BLv1
(2)ab棒的速度大小为
v0,方向向右.1 2
