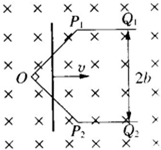
如图所示,OP1Q1与OP2Q2是位于同一水平面上的两根金属导轨,处在沿竖直方向的匀强磁场中,磁感应强度为B,长度相等的导轨OP1段与OP2段相互垂直,交于O点.导轨的P1Q1与P2Q2段相互平行,相距为2b.一根质量为m的金属细杆,在t=0s时从O点出发,在外力作用下以恒定的速度v沿导轨向右滑动.在滑动的过程中,杆始终保持与导轨的平行段相垂直,速度方向与导轨的平行段相平行,杆与导轨有良好的接触.假定导轨与金属杆都有电阻,且每单位长度的电阻都是r.不计金属细杆与轨道之间的摩擦.
(1)金属杆在正交的OP1、OP2导轨上滑动时,通过金属杆中的电流多大?
(2)当t=时,金属杆受到的安培力多大?
(3)从开始运动到t=过程中,外力一共做了多少的功?
(4)若控制外力,使金属杆从静止开始作匀加速直线运动,加速度始终为a,试写出外力随时间变化的规律.
(1)切割产生的感应电动势E=BLV,回路中的电阻R=(2Vt+2Vt)r,
根据欧姆定律得:
I1===
(2)当t=时,导体棒的有效长度为2b,回路中的总电阻为R=(2b+4b)r,
根据欧姆定律得:
I2===
则安培力的大小:FA=BI2L=B•2b=.
(3)根据动能定理得:WF-WA=0
WF=WA=•b=B2b•b=.
(4)分两段讨论:
①0≤t≤
S=at2,V=at,I1=.
F1-BI1•2S=ma
F1=ma+t3.
②t>
R=r=(2b+at2)r
I2==
F2=ma+.
答:(1)金属杆在正交的OP1、OP2导轨上滑动时,通过金属杆中的电流为.
(2)当t=时,金属杆受到的安培力为.
(3)从开始运动到t=过程中,外力一共做功为.
(4)当0≤t≤,F1=ma+t3.当t>时,F2=ma+.